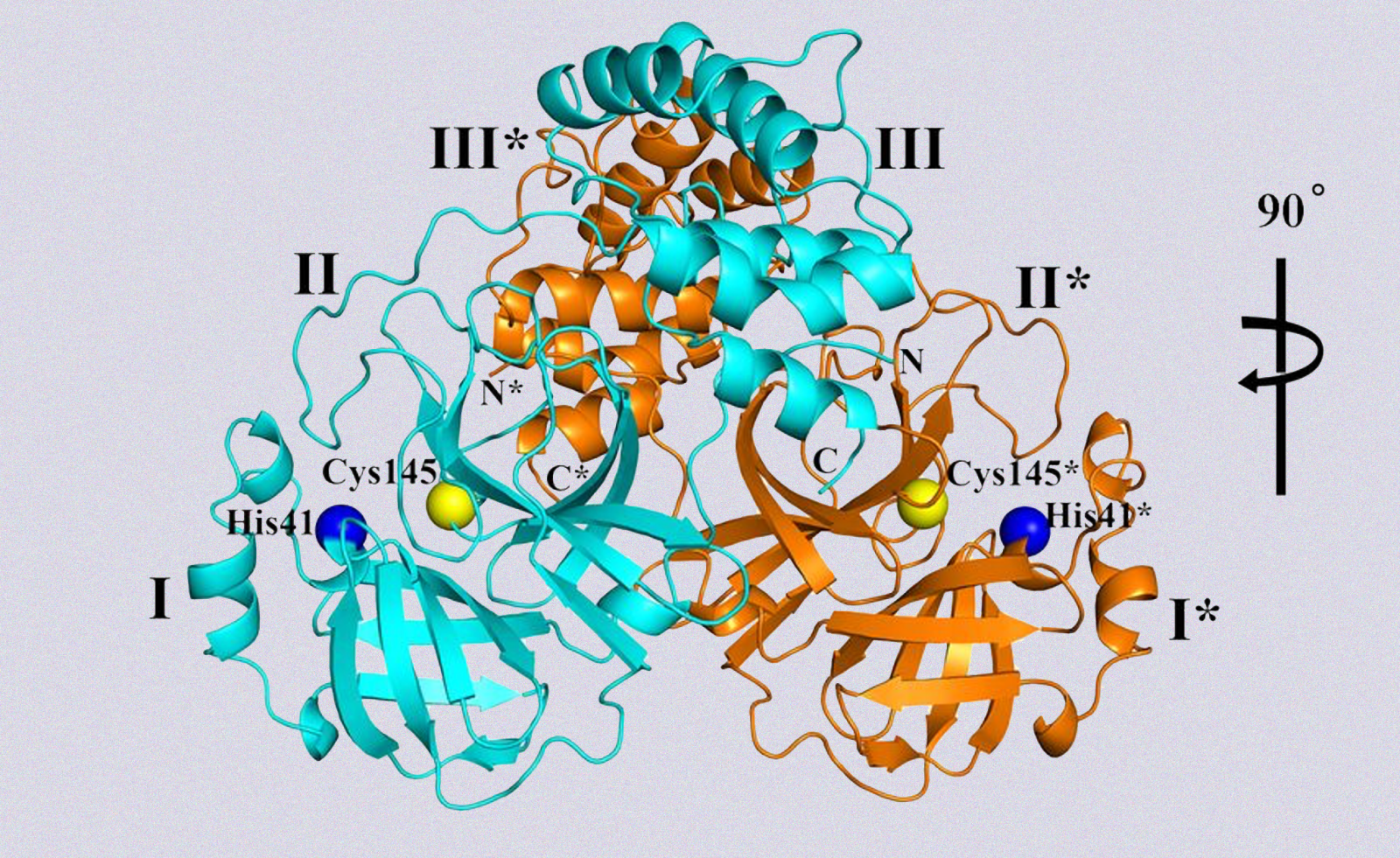
Parte della struttura cristallina, a risoluzione 1,75 Å, dell'enzima della proteasi del coronavirus SARS-CoV-2. Da Science.
Sono sempre le proteine a giocarsi i ruoli fondamentali nei processi chimici e biologici del nostro organismo. Possono avere nomi diversi, ma sempre di proteine si tratta. Una settimana fa, sulla rivista Science, è stato pubblicato lo studio di un ampio team, guidato dal virologo Rolf Hilgenfeld dell'Università di Lubecca, che ha decodificato la struttura tridimensionale (3D) di una speciale proteina, detta proteasi principale di SARS-CoV-2.
Raggi X per realizzare un cristallo della proteasi virale
I ricercatori hanno utilizzato un fascio di raggi X ad alta intensità della struttura BESSY II, il sincrotrone di terza generazione che si trova all'Helmholtz-Zentrum di Berlino. Il sincrotrone è un tipo di acceleratore di particelle molto versatile, che può essere usato per diversi esperimenti. In particolare, è largamente usato per studiare la struttura delle molecole e dei materiali, tra cui le proteine come in questo caso, e consentire lo sviluppo di nuovi medicinali. Gli autori di questo studio, infatti, si sono serviti di BESSY II, per realizzare il modello cristallino della proteasi principale, un enzima che svolge un ruolo essenziale nel ciclo vitale di un virus.
Tagliare per replicarsi
Ma per capire quale sia la funzione di questo enzima, bisogna partire dall'origine. Un virus nasce grazie alla formazione di un lungo filamento di proteine: esse si legano in sequenza, formando una catena chiamata poliproteina. Per poter aggredire le cellule, tuttavia, il virus dovrà essere in grado di replicarsi. È qui che entra in gioco la proteasi (in questo caso Mpro, 3CLpro), che ha il compito di tagliare la lunga catena in più parti, ognuna con una determinata lunghezza: nel caso del Covid, l'enzima compie undici tagli, dividendo il filamento in dodici frammenti. Inizia così il processo di maturazione del virus, che sarà in grado di replicarsi in altre cellule.
Inibire il taglio, quindi l’infezione
Ma perché il virus sia in grado di diffondersi nelle cellule, la proteasi dovrà tagliuzzare la poliproteina in tempi ben precisi, altrimenti la catena verrà distrutta prima ancora che il virus si costruisca. E qui arriviamo al punto: la vulnerabilità di questo passaggio fa della proteasi principale il miglior bersaglio per la terapia farmacologica. In altre parole, l'obiettivo sarà trovare un farmaco che blocchi l'azione di taglio della proteasi, evitando così la trasformazione e diffusione del virus nelle cellule. Da dove cominciare?
Disegnare un nuovo farmaco
Per rendere possibile la realizzazione di un farmaco inibitore, bisogna innanzi tutto conoscere la forma della proteasi, ovvero dell'enzima che ha il compito di tagliare la poliproteina. Ed è qui che il team di Rolf Hilgenfeld ha agito. La conoscenza della forma della proteasi consente la realizzazione di un farmaco inibitore che abbia una ben determinata struttura tridimensionale. In questo caso, è stato scoperto dai ricercatori che la molecola capace di inibire la proteasi e quindi bloccare la riproduzione del virus nelle cellule, si chiama 13b.
Imbrogliare l’enzima
Ma perché è tanto importante l'architettura della molecola inibitrice? Un inibitore deve essere in grado di sostituirsi alla poliproteina, imitandola e legandosi all'enzima allo stesso modo. La sua struttura molecolare deve essere quindi vagamente simile a una proteina, ma con una composizione chimica diversa. Solo così sarà in grado di imbrogliare l'enzima, che al momento della catalisi non riuscirà a tagliarlo, e a evitare il replicarsi del virus nelle cellule. L'architettura 3D fornisce, quindi, dei punti di partenza concreti per lo sviluppo di sostanze attive o di inibitori.
Largo agli inibitori
Già in passato abbiamo assistito alla creazione di farmaci inibitori: lo stesso Rolf Hilgenfeld aveva già sviluppato un inibitore contro il virus SARS durante la pandemia di SARS del 2002/2003 e nel 2016 aveva decifrato un enzima del virus Zika. Senza dimenticare i diversi inibitori dell'Hiv realizzati nel tempo, sebbene in questo caso la struttura dell'enzima abbia un diverso grado di complessità e non risulti ancora del tutto codificabile.
Passerà del tempo, prima di poter vedere un farmaco in grado di ammansire questo virus. Ma gli studi proseguiranno e, come ci dimostra il gruppo di Rolf Hilgenfeld, anche i virus hanno i loro talloni di Achille. E come Paride, dovremo essere in grado di colpirlo.
Fonte
Linlin Zhang et al., Crystal structure of SARS-CoV-2 main protease provides a basis for design of improved α-ketoamide inhibitors. Science 20 Mar 2020.


