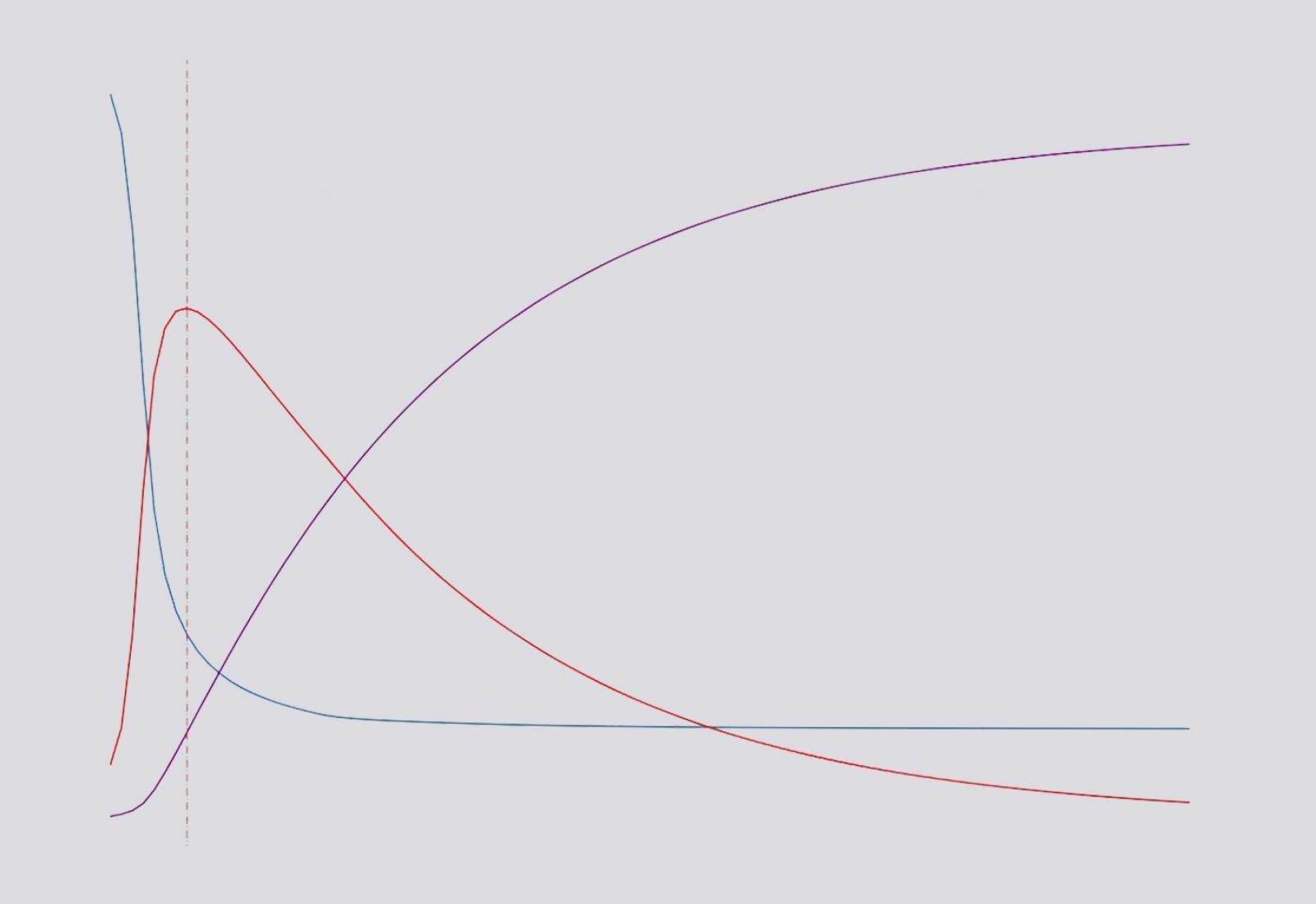
Modello SIR. Sulle ordinate la popolazione, sulle ascisse i giorni. Linea blu, suscettibili; linea rossa, infetti; linea viola, guariti.
Siamo ormai alla fase due, e tutti si domandano come stanno davvero le cose e quanto sia rischiosa la riapertura.
Vi sono in rete vari metodi per valutare questi rischi.
Per lo più si tratta di modelli statistici che usano il metodo della regressione statistica, derivando l’andamento dei nuovi casi osservati nel tempo sulla base dei dati dei giorni precedenti. Siccome questi metodi che non assumono nessun meccanismo specifico legato all’ epidemia, la loro capacità di anticipare l’andamento dei dati è limitata.
E’ invece proprio questo aspetto l’elemento di forza dei modelli epidemiologici.
Introdotti per la prima volta da Daniel Bernouilli nella seconda meta del settecento per studiare l’epidemia di vaiolo e sviluppati in modo sistematico negli anni venti del secolo scorso, questi metodi introducono relazioni tra le variabili osservate che possono dare un aiuto significativo nell’anticipare l’andamento futuro dai dati raccolti in passato.
Come diceva Auguste Compte: “Vedere per prevedere, prevedere per provvedere”.
Cosa ci possono insegnare i modelli epidemiologici nel caso del COVID19? Come possiamo vedere nel seguito possono essere molto utili.
Uno dei modelli più semplici si chiama SIR. La popolazione sotto studio viene divisa in tre categorie: Suscettibile, Infetto, Risolto (da cui il nome SIR ). La matematica del modello permette di capire come nel tempo una parte crescente della popolazione Suscettibile diventa Infetta e come nel tempo gli Infetti diventano Risolti (vale a dire Guariti o Deceduti).
Le equazioni modellano processi dell’epidemia: confrontandoli con i dati e ottimizzando i parametri del modello, si può misurare la forza del virus, la dimensione della popolazione sottoposta all’epidemia, i tempi caratteristici di guarigione o di decesso.
Una volta verificati questi parametri confrontandoli con i dati, è piuttosto facile estrapolare l’andamento futuro: la precisione che si raggiunge è maggiore di quanto non si faccia con una semplice regressione statistica.
Per cercare di capire meglio le dinamiche del Covid-19, in queste settimane ho adattato la modellistica SIR alle condizioni di lockdown e la ho confrontatia con i dati regionali italiani: la versione originale del SIR infatti descrive una epidemia che si sviluppa liberamente, situazione diversa da quella attuale.
Per iniziare a capire i risultati di questo modello, applichiamolo a Wuhan e in Austria, due casi, diversi, ma che possiamo considerare un successo dell’intervento per arrestare l’epidemia.
In figura 1 sono riportati i dati degli Infetti (Totale dei Casi meno i Guariti e meno i Deceduti) e dei Risolti (Guariti + Deceduti) a Wuhan. Durante il lockdown gli Infetti hanno raggiunto il massimo a circa 35 giorni dall’inizio, l’ultimo contagio è stato osservato a 70 giorni dall’inizio. In totale la popolazione coinvolta in questa fase dell’epidemia è stata di circa 80.000 persone su circa 10.000.000. Stiamo parlando di una città paragonabile alle dimensioni della Lombardia. Queste 80.000 persone sono state tracciate e isolate in modo estremamente rigoroso, riuscendo a spegnere l’epidemia poco più di 2 mesi dall’inizio.

Figura 1. Il caso di Wuhan, dati giornalieri modellati con il modello epidemiologico SIR.
Un secondo caso è quello dell’Austria. In figura 2 vediamo l’andamento in corso. Notiamo che la curva degli Infetti decresce ancora più rapidamente che a Wuhan e che probabilmente arriverà alla fine del contagio intorno al 60-mo giorno dall’ inizio dell’ epidemia. Per capirci, l’Austria ha poco meno degli abitanti della Lombardia.

Figura 2. Il caso dell’Austria, dati giornalieri modellati con il modello epidemiologico SIR.
Passiamo alle regioni italiane: per queste analisi ho usato i dati della Protezione civile fino alla fine di aprile.
Cerchiamo innanzitutto di capire la capacità predittiva del modello SIR adattato al lockdown. Per questo ho applicato l’analisi in 7 periodi diversi a partire dal lockdown, assunto il 10 marzo: 2, 3, 4, 5, 6, 7 e 8 settimane successive al 10 marzo.
Da ognuna di queste analisi ricaviamo la predizione del modello, che poi viene estrapolata nel futuro. Facciamo un esempio, con i dati dal 10 marzo al 23 marzo, calcolo i parametri del modello che poi posso confrontare con i dati già raccolti fino a fine aprile. Lo stesso lo faccio poi con i dati dal 10 marzo al 30 marzo e così via per sette volte.
Il risultato è riportato nelle grafici più sotto.
Ogni riga rappresenta una regione, ogni colonna l’intervallo di tempo usato per calcolare i parametri del modello.
Nella prima colonna, le curve del modello riescono a descrivere solo i dati raccolti fino al giorno 20 marzo: da lì in poi i dati hanno un andamento molto diverso dalle predizioni del modello. C’è però una eccezione, l’Umbria, dove già con i dati fino al 20 marzo è possibile prevedere il massimo della curva degli Infetti che avverrà circa 10 giorni dopo. Questa regione, due settimane dopo il lockdown già stava seguendo un andamento epidemiologico SIR!
Continuando colonna per colonna, vediamo che, in modo sistematico, quando i dati osservativi raggiungono il massimo del numero degli Infetti, il modello SIR si “aggancia” all’andamento dei dati e produce delle curve che predicono l’andamento nei giorni successivi.

Figura 3. Abruzzo, Basilicata, Calabria, Campania, Emilia Romagna, Friuli Venezia Giulia.

Figura 4. Lazio, Liguria, Lombardia, Marche, Molise, P.A. Bolzano.

Figura 5. P.A. Trento, Piemonte, Puglia, Sardegna, Sicilia, Toscana.

Figura 6. Umbria, Valle d'Aosta, Veneto.
A partire dalla 4a settimana, il Friuli Venezia GIulia, poi, 5a settimana, Basilicata, Campania, Marche, Trentino, Sardegna, Valle D’Aosta e Veneto, poi , 6a settimana, Toscana, Molise, Calabria, Emilia-Romagna, Bolzano, poi, 7a settimana, Abruzzo e Sicilia e infine, 8a settimana, il Lazio, le curve del modello iniziano a predire i dati del periodo successivo con sempre maggiore precisione. Ci sono ancora 4 regioni italiane, Lombardia, Piemonte, Liguria e Puglia, che alla data della fine del lockdown non hanno raggiunto il massimo della curva degli Infetti.
Cosa possiamo dedurre da questa analisi:
- Il modello epidemiologico SIR hanno capacità predittiva anche nella condizione di lockdown.
- La risposta delle regioni italiane è differenziata per quanto riguarda i dati dell’epidemia: alcune rispondono immediatamente seguendo la descrizione del modello SIR fin dalle prime settimane, altre rispondono con ritardi variabili, che possono superare i due mesi dal lockdown.
- La causa della differenza è molto probabilmente dovuta all’efficacia del lockdown. Dove il lockdown è meno efficace, l’infezione continua a svilupparsi, anche se con un indice di riproduzione Refficace più basso di 1. Infatti dopo avere raggiunto il massimo del numero di Infetti, l’epidemia si spegne. Tanto più questo indice Refficace è vicino a 1 tanto più tardi avviene l’aggancio con l’andamento del modello epidemiologico.
- In quattro regioni non siamo ancora arrivati a definire quando si avrà il massimo degli infetti e questo rende l’imminente riapertura più pericolosa rispetto a regioni in cui la decrescita è ormai in atto. Non siamo nemmeno certi che in quelle regioni Reffettivo sia minore di 1.
I risultati ottenuti tendono inoltre a smentire il modello di una semplice propagazione del virus dal Nord-Ovest al Sud, evidenziando piuttosto differenze nelle modalità con cui le varie regioni hanno affrontato l’emergenza sanitaria. Un’ulteriore conferma che regionalizzazione della Sanità italiana tende a dominare rispetto alle dinamiche del virus.
Mi auguro che questo articolo ci abbia aiutato a capire l’utilità dei modelli epidemiologici nella strategia di contrasto al COVID19.



