Dopo le “riaperture” di maggio e inizio giugno 2020, l’epidemia di coronavirus in Italia negli ultimi due mesi è stata caratterizzata dalla progressiva comparsa di focolai da nord a sud del paese, che le autorità sanitarie riescono a circoscrivere nell’arco di una/due settimane (vedi Figura 1 di questo articolo). La molteplicità dei focolai, il cui numero sta crescendo in modo esponenziale (vedi articolo), genera nella stragrande maggioranza delle regioni italiane un aumento di tipo esponenziale del numero totale dei casi positivi. In questa nota, tale aumento viene analizzato nelle 10 settimane dal 1 giugno al 9 agosto 2020 e caratterizzato sia a livello qualitativo che quantitativo.
Le tre regioni italiane meno popolose, la Basilicata, il Molise e la Valle D’Aosta mostrano un andamento crescente “a salti” del numero totale dei casi registrati (vedi Figure 1-3). La situazione è molto diversa nelle regioni con grande popolazione. In questo caso l’andamento è ben descritto da un modello matematico di tipo esponenziale, come illustrato nelle Figure 4-18 per le regioni Abruzzo, Calabria, Campania, Emilia-Romagna, Friuli-Venezia Giulia, Marche, Piemonte, Puglia, Sardegna, Sicilia, Toscana, Umbria e Veneto e per le province autonome di Bolzano e Trento.

Figura 1 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Basilicata nel periodo dal 1 giugno al 9 agosto 2020.

Figura 2 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Molise nel periodo dal 1 giugno al 9 Agosto 2020.

Figura 3 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Valle D’Aosta nel periodo dal 1 giugno al 9 agosto 2020.

Figura 4 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Abruzzo nel periodo dal 15 giugno al 9 agosto 2020.

Figura 5 Andamento temporale del numero totale di casi registrati positivi al coronavirus nella provincia autonoma di Bolzano nel periodo dal 1 giugno al 9 agosto 2020.

Figura 6 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Calabria nel periodo dal 15 giugno al 9 agosto 2020.

Figura 7 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Campania nel periodo dal 15 giugno al 9 agosto 2020.

Figura 8 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Emilia Romagna nel periodo dal 1 giugno al 9 Agosto 2020.

Figura 9 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Friuli Venezia Giulia nel periodo dal 15 giugno al 9 agosto 2020.

Figura 10 Andamento temporale del numero totale di casi registrati positivi al coronavirus nelle Marche nel periodo dal 6 luglio al 9 agosto 2020.

Figura 11 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Piemonte nel periodo dal 13 luglio al 9 agosto 2020.

Figura 12 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Puglia nel periodo dal 22 giugno al 9 agosto 2020.

Figura 13 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Sardegna nel periodo dal 13 luglio al 9 agosto 2020.

Figura 14 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Sicilia nel periodo dal 15 giugno al 9 agosto 2020.

Figura 15 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Toscana nel periodo dal 15 giugno al 9 agosto 2020.

Figura 16 Andamento temporale del numero totale di casi registrati positivi al coronavirus nella provincia autonoma di Trento nel periodo dal 15 giugno al 9 agosto 2020.

Figura 17 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Umbria nel periodo dal 15 giugno al 9 agosto 2020.

Figura 18 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Veneto nel periodo dall’8 giugno al 9 agosto 2020.
L’intervallo di tempo effettivamente considerato è quello che termina il 9 agosto e inizia il prima possibile (quindi l’intervallo ha ampiezza massima) e che ha il miglior adattamento del modello ai dati. Sovrapposto ai dati, abbiamo rappresentato anche il miglior fit con un modello esponenziale del tipo Yt =Y0 +Ŷ*(2t/τ-1), dove Y0 è il valore al tempo zero, Ŷ e τ sono due costanti positive (vedi Figura 6 in di questo articolo). Il parametro τ è noto come “tempo di raddoppio”; più il suo valore è piccolo, più velocemente cresce Yt. Nonostante per alcune regioni siano evidenti le “onde” della sequenza misurata dovute ai focolai, c’è un buon adattamento su grande scala temporale del modello ai dati. I valori stimati dei tempi di raddoppio per le diverse regioni italiane sono riportati in Tabella 1.
Osserviamo che alcuni dei valori più bassi del tempo di raddoppio sono molto vicini a quelli relativi a stati europei come la Spagna (9 giorni) ed il Belgio (10 giorni) dove al momento il virus si diffonde molto velocemente e dove è stato necessario introdurre nuovamente, seppure a livello locale, delle misure di lockdown. Alla luce del contributo non trascurabile alla diffusione dell’epidemia da parte delle persone che arrivano in Italia dall’estero, sarebbe opportuno rafforzare i controlli negli aeroporti e sui soggetti che devono effettuare la quarantena.
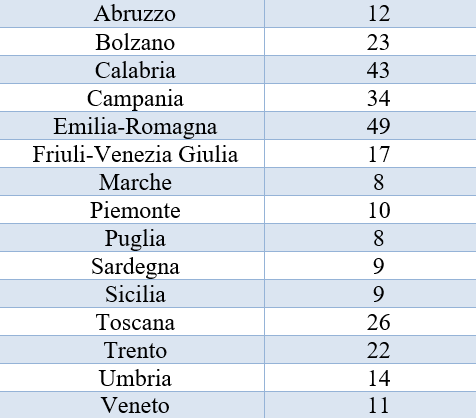
Tabella 1 Valori del tempo di raddoppio (in giorni) del modello esponenziale stimato a partire dalla sequenza temporale del numero totale dei casi positivi al coronavirus per le diverse regioni italiane.
Nelle tre regioni restanti, Lazio, Liguria e Lombardia, la crescita del numero totale dei contagi nell’ultimo periodo è di tipo lineare (vedi Figure 19-21). Questo si può spiegare con una crescita più lenta del numero di focolai e con un modo più efficacie di circoscriverli. A questo riguardo, invito una volta ancora tutti gli italiani a scaricare ed utilizzare l’app Immuni (vedi qui). L’invito è rivolto in particolare ai giovani che di recente stanno contribuendo in modo tutt’altro che trascurabile alla diffusione del virus nel nostro paese, fenomeno che accade anche in altri stati. Questo è dimostrato dall’età media dei contagiati che si è abbassata da un valore di circa 60 anni nei mesi iniziali di diffusione del virus in Italia a 40-45 anni.

Figura 19 Andamento temporale del numero totale di casi registrati positivi al coronavirus nel Lazio nel periodo dal 22 giugno al 9 agosto 2020.

Figura 20 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Liguria nel periodo dal 13 luglio al 9 agosto 2020.

Figura 21 Andamento temporale del numero totale di casi registrati positivi al coronavirus in Lombardia nel periodo dal 13 luglio al 9 agosto 2020.
In Italia la sintomatologia dei casi, compresi quelli relativi ai giovani, sembra che al momento sia di tipo lieve-medio o addirittura assente. Questo non è però vero in generale, come mostra ad esempio quello che accade al momento in Israele. Oltre ai danni respiratori e di altro genere che l'infezione può provocare anche nei giovani, il contagio tra i giovani contribuisce alla diffusione del virus ed aumenta il rischio che esso raggiunga le categorie “fragili”, come quella delle persone anziane, spesso affette da una o più malattie concomitanti.
La trasmissione del virus ai soggetti fragili può accadere ad esempio in ospedale o in strutture di lungodegenza, così come in ambito familiare. A questo scopo è utile ricordare il risultato dell’indagine di sieroprevalenza dell’Istat e del Ministero della Salute secondo il quale la probabilità di essere infettati sale dal 2.5% al 42% se si è stati a contatto con un familiare convivente affetto dal virus (vedi articolo sull'indagine di sieroprevalenza). Vale quindi l'invito a tutti, in particolare ai giovani, ad usare tutte le misure possibili per limitare la diffusione del virus.
Nelle Figure 22-26, mostriamo la distribuzione spaziale dell’incidenza bi-settimanale per 100,000 abitanti dal 1 giugno al 9 agosto 2020. La scala dei toni di grigio è la stessa per ciascuna mappa. Oltre al confronto dei valori dell’incidenza nelle varie regioni relativi a una fissata coppia di settimane consecutive, è quindi possibile anche quello dei valori dell’incidenza della stessa regione relativi a intervalli di tempo diversi. In ciascuno dei cinque intervalli, i valori dell’incidenza nelle regioni del nord sono in media maggiori di quelli relativi al sud. Osserviamo che per la Lombardia, il valore dell’incidenza nel periodo dal 1 al 14 giugno è maggiore di quello relativo al periodo dal 15 al 28 giugno.

Figura 22 Mappa delle regioni italiane con l’intensità decrescente al crescere dell’incidenza per 100,000 abitanti dal 1 al 14 giugno 2020.
 Figura 23 Mappa delle regioni italiane con l’intensità decrescente al crescere dell’incidenza per 100,000 abitanti dal 15 al 28 giugno 2020.
Figura 23 Mappa delle regioni italiane con l’intensità decrescente al crescere dell’incidenza per 100,000 abitanti dal 15 al 28 giugno 2020.

Figura 24 Mappa delle regioni italiane con l’intensità decrescente al crescere dell’incidenza per 100,000 abitanti dal 29 giugno al 12 luglio 2020.

Figura 25 Mappa delle regioni italiane con l’intensità decrescente al crescere dell’incidenza per 100,000 abitanti dal 13 luglio al 26 luglio 2020.

Figura 26 Mappa delle regioni italiane con l’intensità decrescente al crescere dell’incidenza per 100,000 abitanti dal 27 luglio al 9 agosto 2020.
L’incidenza decresce passando prima al periodo dal 29 giugno al 12 luglio, e poi a quello dal 13 al 26 luglio; quest’ultimo valore è invece molto simile a quello del periodo dal 27 luglio al 9 agosto. Per l’Emilia-Romagna invece l’incidenza cresce tra il primo e il secondo intervallo di tempo, rimane poi più o meno costante dal secondo al terzo intervallo, per poi aumentare dal terzo al quarto e infine rimanere invariato passando al quinto intervallo.
Come per la Lombardia, anche nel Veneto l’incidenza è confrontabile nei primi due intervalli di giugno, mentre nei successivi tre intervalli l’incidenza è in progressiva crescita. Il progressivo aumento dell’incidenza negli ultimi tre intervalli avviene anche in Sicilia. Notiamo infine la crescita dell’incidenza dal penultimo all’ultimo intervallo per Toscana, Marche e Abruzzo, probabilmente per la contiguità con l’Emilia-Romagna delle prime due e della seconda con la terza.
Seppure i valori dell’incidenza nelle regioni del nord siano in media maggiori di quelli a sud, c’è una tendenza all’uniformizzazione della distribuzione degli aumenti nelle varie regioni. Questo può essere apprezzato dalla Figura 27 che mostra l’andamento temporale crescente del reciproco del “coefficiente di variazione” (rapporto tra deviazione standard e valor medio) dell’incidenza nelle varie regioni.

Il progressivo aumento del numero totale dei casi, assieme all’uniformizzazione a livello nazionale, è quello che sarebbe accaduto, su una scala notevolmente maggiore, se a marzo non avessimo effettuato il lockdown a livello nazionale. Qualsiasi modello matematico per la diffusione di epidemie, dal più semplice al più raffinato, in assenza di altri interventi, come ad esempio la vaccinazione, prevede questo [1].

Figura 27 Andamento del reciproco del “coefficiente di variazione” (rapporto tra deviazione standard e valor medio) dell’incidenza bi-settimanale regionale dal 1 giugno al 9 agosto 2020.
Note
1. Ciascuno è libero di credere quello che vuole, perfino che la matematica non debba essere utilizzata in questo contesto, come di recente è stato affermato in ambito medico. Forse sarebbe opportuno rendersi conto di quanto, seppure “invisibile”, la matematica sia presente nella nostra quotidianità: alla base di una TAC c’è la “trasformata” di Radon (introdotta da Radon 50 anni prima, il che illustra bene l’importanza della ricerca di base); facciamo una RM senza sapere che alla base c’è un’altra trasformata, quella di Fourier; ogni volta che usiamo il bancomat, i numeri primi ci permettono di farlo in sicurezza; quando usiamo il navigatore in macchina dobbiamo essere grati a Dijkstra per il suo algoritmo; sì ma allora dobbiamo farlo anche con Markov per le sue “catene” quando otteniamo una lista ordinata di nomi di siti dopo aver interpellato Google (il cui nome originario, secondo la versione ufficiale, era googol, che è il nome del numero composto da 1 seguito da 100 zeri; a causa di un errore, il nome venne registrato come Google e successivamente mantenuto).


