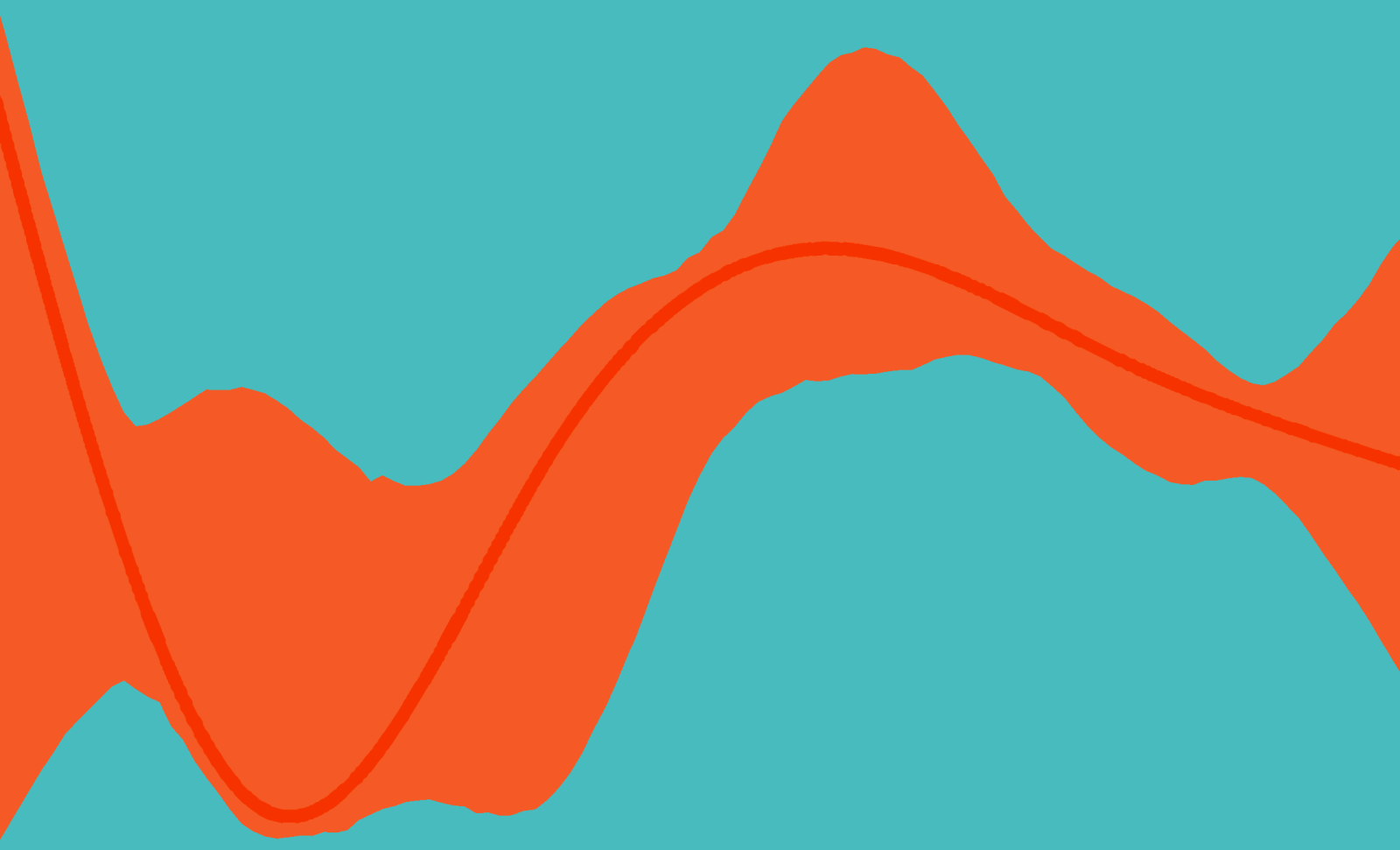
Curva stimate (e incertezza attorno alla stima) di R0(t) in Friuli Venezia Giulia, 1 agosto-30 novembre.
Tratto da Giulia Cereda, Cecilia Viscardi, Luca Gherardini, Fabrizia Mealli, Michela Baccini (2020). A SIRD model calibrated on deaths to investigate the second wave of the SARS-CoV-2 epidemic in Italy. E&P Repository https://repo.epiprev.it/2052
Tra i 21 dibattuti indicatori calcolati dall'Istituto Superiore di Sanità per classificare le regioni nei tre livelli di allarme (giallo, arancione e rosso), c’è il numero di riproduzione dell’infezione, che corrisponde al numero medio di contagi generati da un singolo infetto. L’ISS aggiorna periodicamente l’indice, noto come Rt (e che equivale a quello che qui noi chiameremo R0(t)), basandosi sul numero di infezioni sintomatiche osservate. Purtroppo i dati utilizzati per la stima di questo e degli altri indicatori non sono resi pubblici, e questo impedisce alla comunità scientifica di riprodurre le stime dell’ISS e di proporre alternative.
Ampliando lo studio già intrapreso per la Toscana sui dati della prima ondata epidemica, abbiamo pertanto usato le uniche informazioni disponibili, ovvero i dati forniti dalla Protezione Civile (https://github.com/pcm-dpc/COVID-19), per produrre in autonomia le stime di R0(t) e del numero di infetti circolanti per ciascuna regione dall’1 agosto al 30 novembre 2020. I dati della Protezione Civile non sono individuali, sono conteggi giornalieri, non contengono indicazioni relative alla sintomaticità degli infetti notificati e ad altre caratteristiche importanti, come l’età dei positivi. Il numero giornaliero di decessi COVID19 è, tra le informazioni messe a disposizione, quella più affidabile, meno affetta da ritardi di registrazione, ma soprattutto non dipende, come invece il numero di positivi, dal numero di test molecolari effettuati.
Concentrandoci dunque sul numero di decessi, il modello statistico che abbiamo utilizzato è basato su un’idea semplice. Giorno per giorno la popolazione è suddivisa in 4 gruppi o compartimenti (da cui il nome di modello compartimentale): i suscettibili (che possono essere contagiati), gli infetti (che hanno contratto il virus e possono trasmettere il contagio), i guariti e i deceduti COVID19. Nel corso del tempo, gli individui possono passare da un compartimento all’altro e la probabilità di farlo dipende da alcune quantità di cui si è spesso sentito parlare. Per esempio, la letalità dell’infezione regola il passaggio da infetto a deceduto, R0(t) regola invece il passaggio da suscettibile a infetto perché esprime la forza del contagio. Fissata la letalità all’1,14% (un valore sovrapponibile a quello stimato per i paesi ad alto reddito in un recente report dell’Imperial College) e il tempo medio che intercorre tra infezione e morte o guarigione a 14 giorni, abbiamo usato un algoritmo di calibrazione per trovare la curva di R0(t) che meglio riproducesse il dato di mortalità riportato dalla Protezione Civile, valutandone anche l’incertezza statistica. Questo, per tutte le regioni italiane.
In figura 1 mostriamo le curve stimate di R0(t); le bande grigie indicano l’incertezza attorno alla stima. Dato che i decessi secondo il nostro modello si verificano in media 14 giorni dopo il contagio, le informazioni alla fine della curva sono scarse. La linea rossa indica il valore R0(t)=1, al di sotto del quale l’epidemia tende ad esaurirsi (il numero dei nuovi infetti è inferiore a quello delle guarigioni).
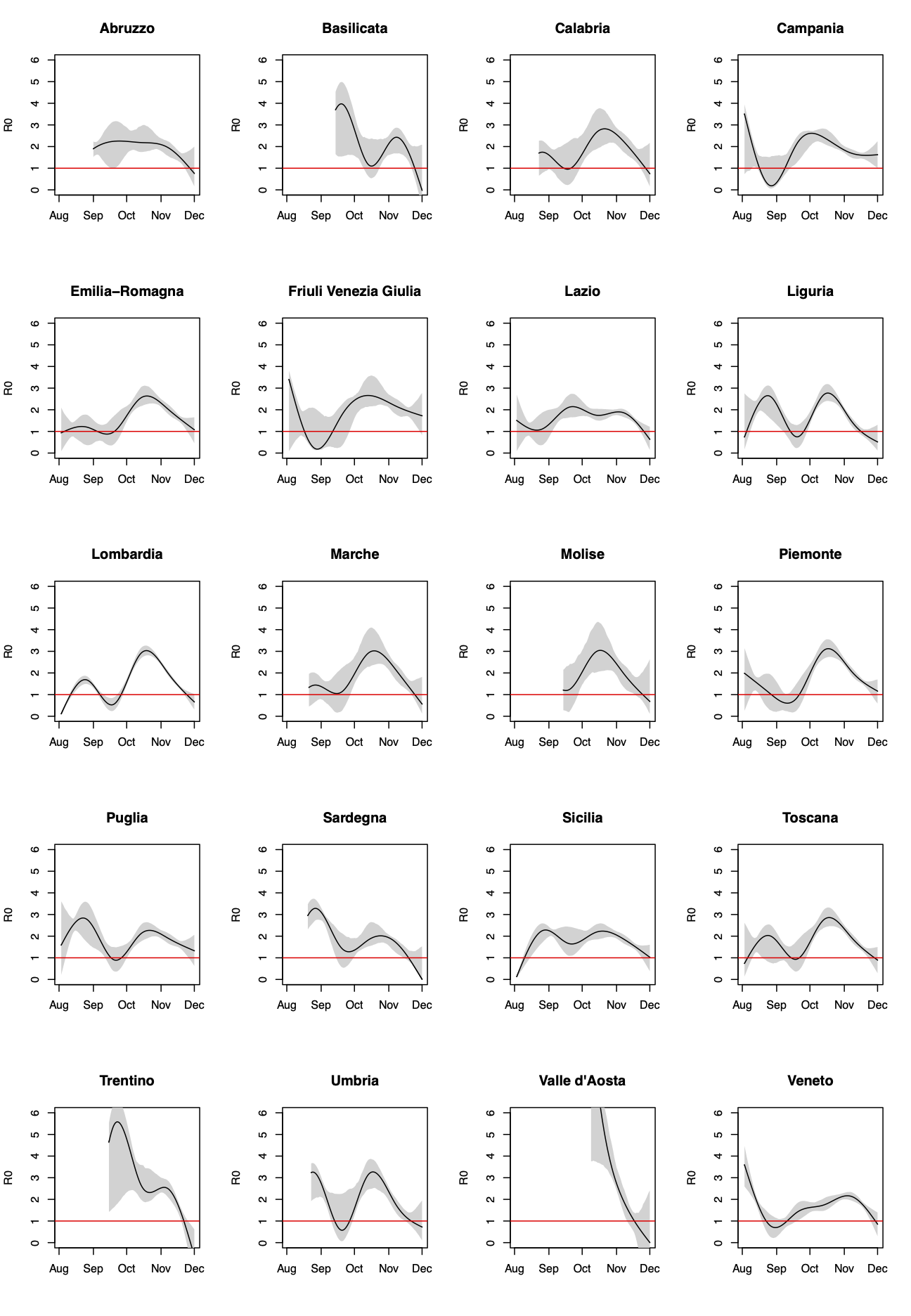
Figura 1. Stime di R0(t) con bande di confidenza al 90% per tutte le regioni italiane per il periodo 1 agosto-30 novembre.
L’andamento temporale di R0(t) è eterogeneo tra le regioni. Tuttavia in molti casi è visibile un picco a metà/ fine ottobre, al culmine di una crescita iniziata nella prima metà di settembre. Dopo l’indice scende, per raggiungere a fine novembre valori vicini o inferiori a 1 in tutte le regioni, escluse Campania, Friuli Venezia Giulia e Puglia, dove resta, in modo più o meno evidente, sopra 1.
Ci preme sottolineare che l’analisi condotta non consente di individuare i fattori che hanno generato le variazioni di R0(t) nel tempo, ma è difficile non sospettare che la scuola possa aver innescato o almeno contribuito alla crescita del contagio a settembre, insieme alla ripresa a regime delle attività lavorative e quindi delle attività di trasporto pubblico. Analogamente è verosimile che la discesa dell’indice a novembre sia stata prodotta dall'introduzione di misure di contenimento nazionali e locali. Tuttavia, è importante osservare che regioni mai classificate come rosse (es. Emilia Romagna) hanno avuto una diminuzione dell’indice paragonabile a quella delle regioni rosse (es. Toscana) e che regioni che sono passate alla zona rossa nella stessa data hanno sperimentato un declino di R0(t) di diversa intensità (es. Toscana e Campania). La curva piuttosto “piatta” del Lazio, con un indice inferiore a 2 per tutto il periodo di studio e senza picchi rilevanti, denota una dinamica epidemica apparentemente diversa da quella del resto del Paese, che potrebbe essere correlata a una maggiore capacità di controllo del contagio. I valori molto alti stimati in ottobre per la Valle d'Aosta e il Trentino Alto Adige, dopo due mesi senza decessi COVID19, potrebbero essere legati a situazioni di super diffusione, che hanno portato in modo repentino a livelli di contagio allarmanti.
Rispetto alle tecniche di analisi che si concentrano sul solo R0(t), il nostro modello produce anche una stima del numero di persone infette presenti in regione giorno dopo giorno. Questa quantità, insieme a R0(t), è utile per valutare l'effettivo impatto dell’epidemia sul sistema sanitario. Infatti, se un R0(t) elevato può essere sostenibile all'inizio dell'epidemia quando il numero di casi è basso, un valore anche basso di R0(t) potrebbe non essere sostenibile quando il numero di infetti circolanti è elevato. Il grafico della figura 2 riporta il numero stimato di infezioni circolanti per 1000 abitanti (non è riportata in questo caso l’incertezza attorno alla stima; per dettagli si rimanda all’articolo completo). Nonostante il calo di R0(t) nella maggior parte delle regioni, il numero di infezioni circolanti stimato non è tuttora trascurabile, in particolare nel Nord del Paese. Ciò suggerisce che anche una piccola crescita di R0(t) potrebbe condurre di nuovo in breve tempo a livelli di contagio insostenibili, a seconda della capacità dei sistemi sanitari regionali di affrontare l'emergenza.
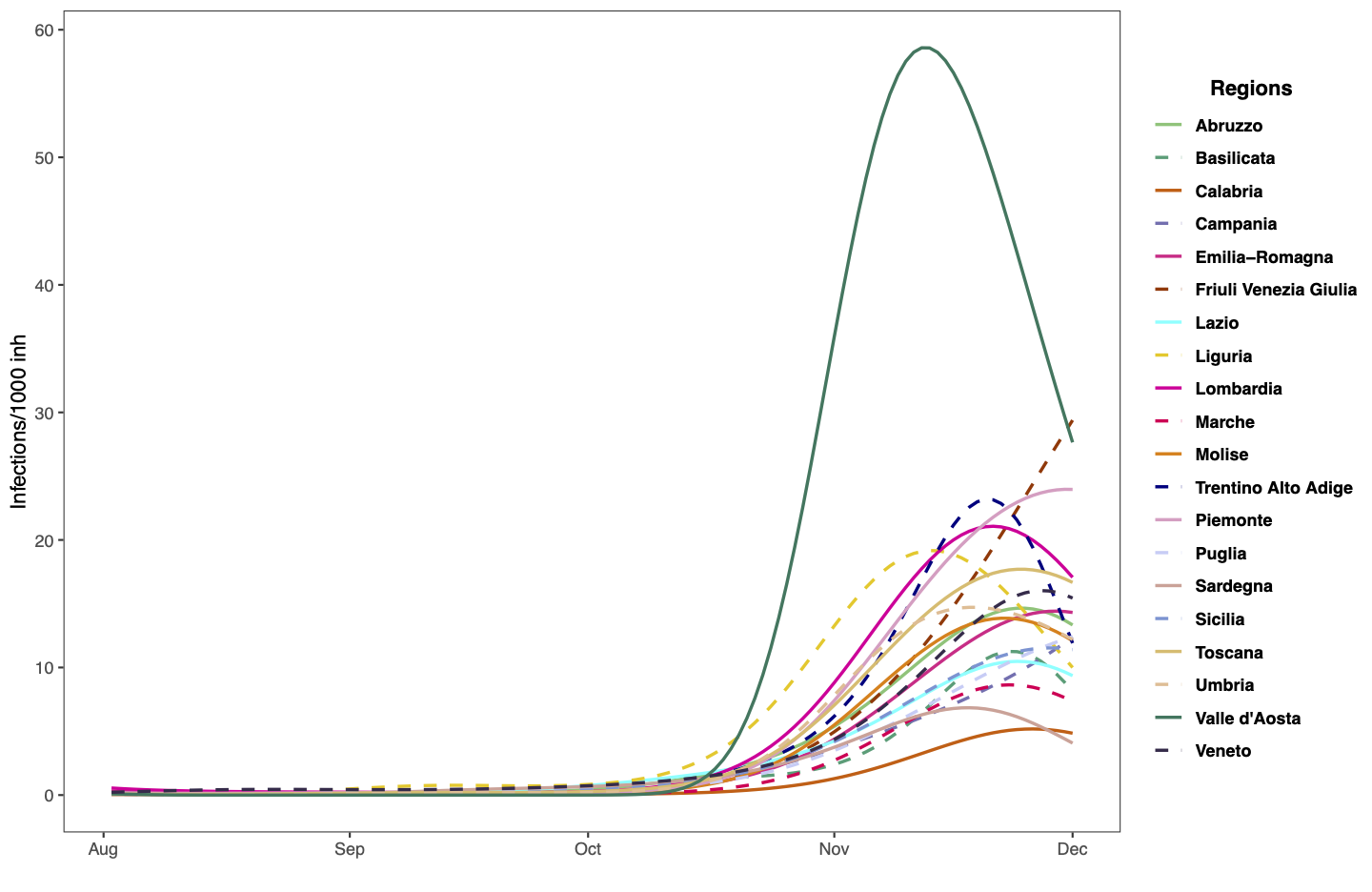
Figura 2. Numero di infezioni presenti nelle regioni ogni 1000 abitanti, assumendo un tasso di letalità dell’infezione pari all’1,14% per il periodo 1 agosto-30 novembre.
Guardare alla velocità di contagio, R0(t), e al numero di infezioni sotto diversi scenari più o meno ottimistici di letalità potrebbe essere uno strumento utile nelle settimane a venire. In un contesto di emergenza in cui ogni stima è destinata a diventare presto obsoleta, provvederemo ad aggiornare le nostre valutazioni e faremo uno sforzo per rendere fruibile il codice utilizzato per le analisi.
Nell’articolo, in inglese, ancora non peer reviewed, visibile sul repository di Epidemiologia & Prevenzione (repo.epiprev.it/2052), sono riportati e discussi in maggiore dettaglio i risultati sotto due scenari di letalità, insieme alle caratteristiche e ai limiti del metodo statistico utilizzato.


